Le reti ricorrenti a memoria a lungo termine (LSTM)

Le reti neurali ricorrenti a memoria a lungo termine (LSTM) sono un tipo di architettura di rete neurale ricorrente (RNN) progettata per gestire il problema della scomparsa del gradiente nelle reti neurali tradizionali durante l'apprendimento di lunghe sequenze di dati, come nel caso del processing del linguaggio naturale (NLP).
Le LSTM sono in grado di mantenere e gestire informazioni a lungo termine attraverso la sequenza temporale, il che le rende particolarmente adatte per compiti che richiedono la comprensione e la generazione di testi, traduzione automatica, analisi del sentiment, e altro ancora.

Le LSTM risolvono il problema della scomparsa del gradiente attraverso l'introduzione di una struttura complessa di celle di memoria che sono in grado di memorizzare e dimenticare informazioni a seconda del contesto e del compito in esame.
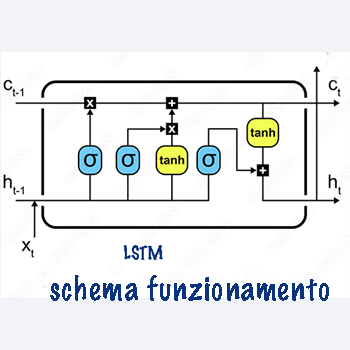
Questa struttura è composta da tre porte principali: la porta di input, la porta di output e la porta di forget, ognuna delle quali regola il flusso delle informazioni attraverso la rete.

Formule e Funzionamento LSTM

Porta di Input (Input Gate)

- La porta di input controlla quanto della nuova informazione viene aggiunta alla cella di memoria.

- Si calcola utilizzando una funzione sigmoidea che trasforma l'input e la memoria dello stato precedente, seguita da una funzione tangente iperbolica che trasforma l'input e lo stato precedente.
Questi due risultati vengono quindi moltiplicati insieme.

- La formula matematica per la porta di input è:
\[ i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \] dove:
- \( i_t \) è il vettore di attivazione della porta di input al tempo \( t \).
- \( \sigma \) è la funzione sigmoidea.
- \( W_i \) e \( b_i \) sono i pesi e il bias della porta di input rispettivamente.
- \( h_{t-1} \) è lo stato nascosto al tempo precedente.
- \( x_t \) è l'input al tempo \( t \).

Porta di Forget (Forget Gate)

- La porta di forget controlla quanto della memoria dello stato precedente viene dimenticato.
- Si calcola utilizzando una funzione sigmoidea che trasforma l'input e la memoria dello stato precedente.

- La formula matematica per la porta di forget è:
\[ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \]
dove:
- \( f_t \) è il vettore di attivazione della porta di forget al tempo \( t \).
- \( \sigma \) è la funzione sigmoidea.
- \( W_f \) e \( b_f \) sono i pesi e il bias della porta di forget rispettivamente.

Cella di Memoria (Memory Cell)

- La cella di memoria memorizza e aggiorna le informazioni attraverso la sequenza temporale.
- La formula matematica per la cella di memoria è:
\[ C_t = f_t \cdot C_{t-1} + i_t \cdot \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \]
dove:
- \( C_t \) è lo stato della cella di memoria al tempo \( t \).
- \( \tanh \) è la funzione tangente iperbolica.
- \( W_C \) e \( b_C \) sono i pesi e il bias della cella di memoria rispettivamente.

Porta di Output (Output Gate)

- La porta di output controlla quanto della cella di memoria viene emesso come output.
- Si calcola utilizzando una funzione sigmoidea che trasforma l'input e la memoria dello stato precedente, seguita da una funzione tangente iperbolica che trasforma l'input e lo stato precedente. Questi due risultati vengono quindi moltiplicati insieme.

- La formula matematica per la porta di output è:
\[ o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \]
dove:
- \( o_t \) è il vettore di attivazione della porta di output al tempo \( t \).
- \( \sigma \) è la funzione sigmoidea.
- \( W_o \) e \( b_o \) sono i pesi e il bias della porta di output rispettivamente.

Output dello Stato Nascosto (Hidden State Output)

- Lo stato nascosto aggiornato è calcolato moltiplicando il vettore di output della porta di output con la funzione tangente iperbolica applicata alla cella di memoria al tempo corrente.
- La formula matematica per lo stato nascosto aggiornato è:
\[ h_t = o_t \cdot \tanh(C_t) \]
dove:
- \( h_t \) è lo stato nascosto aggiornato al tempo \( t \).
- \( \tanh \) è la funzione tangente iperbolica.
- \( C_t \) è lo stato della cella di memoria al tempo \( t \).

Lo schema di funzionamento delle LSTM mostra come le informazioni fluiscano attraverso le varie porte e la cella di memoria.
L'output dello stato nascosto aggiornato viene quindi passato allo strato successivo della rete neurale, consentendo la gestione di sequenze di dati complesse e la preservazione delle informazioni a lungo termine.