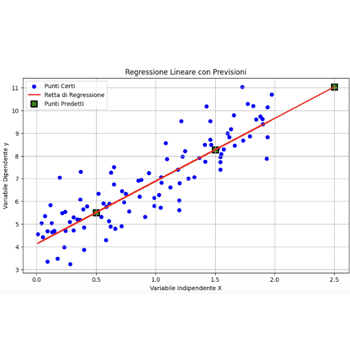
Regressione Lineare
Regressione lineare con linearRegression(). I passi del machine learning
Passi Regressione lineare
Creazione del Dataset
import numpy as np
# Creazione del dataset
np.random.seed(42) # Per riproducibilità
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
print("X:\n", X[:5])
print("y:\n", y[:5])
Suddivisione del Dataset
Utilizziamo `train_test_split` per suddividere i dati in set di training e di test (30%).
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print("X_train:\n", X_train[:5])
print("y_train:\n", y_train[:5])
Costruzione del Modello di Regressione Lineare
Usiamo `LinearRegression` per costruire il modello.
from sklearn.linear_model import LinearRegression
# Costruzione del modello
model = LinearRegression()
model.fit(X_train, y_train)
# Predizioni sul set di test
y_pred = model.predict(X_test)
### Passaggio 4: Validazione dei Risultati
Valutiamo il modello utilizzando le metriche MAE, MSE e \(R^2\).
- MAE (Mean Absolute Error): misura la media degli errori assoluti tra le predizioni e i valori reali. È una misura della precisione degli errori.
- MSE (Mean Squared Error): misura la media degli errori al quadrato tra le predizioni e i valori reali. Penalizza maggiormente gli errori più grandi rispetto alla MAE.
- \(R^2\) (Coefficient of Determination): indica la proporzione della varianza nei dati dipendenti che è prevedibile dalle variabili indipendenti. Un valore di \(R^2\) pari a 1 indica un modello perfetto.
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# Calcolo delle metriche
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"Mean Squared Error (MSE): {mse:.2f}")
print(f"R^2: {r2:.2f}")
Codice Completo
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# Creazione del dataset
np.random.seed(42) # Per riproducibilità
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# Suddivisione del dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Costruzione del modello
model = LinearRegression()
model.fit(X_train, y_train)
# Predizioni sul set di test
y_pred = model.predict(X_test)
# Calcolo delle metriche
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"Mean Squared Error (MSE): {mse:.2f}")
print(f"R^2: {r2:.2f}")
### Risultati Attesi Ecco cosa ci aspettiamo di ottenere come output:
Mean Absolute Error (MAE): 0.70
Mean Squared Error (MSE): 0.66
R^2: 0.92
Questi risultati indicano che il modello di regressione lineare è abbastanza accurato, con un \(R^2\) di 0.92 che mostra una buona proporzione della varianza spiegata dalle variabili indipendenti.