Il teorema di Bayes permette di conoscere la probabilità che si manifesti una causa dato l’effetto finale. Dopo aver stilato la lista delle possibili cause e determinato la probabilità che si manifesti ogni singola causa si stima la probabilità che questo effetto si manifesti data ogni possibile causa.

Ci sono 2 eventi A,B
P(A)-> probabilità a priori di A P(B)-> probabilità a priori di B (P(B) ≠ 0)
P(A|B) La probabilità condizionata di A noto B
P(B|A) La probabilità condizionata di B noto A

Teorema di bayes

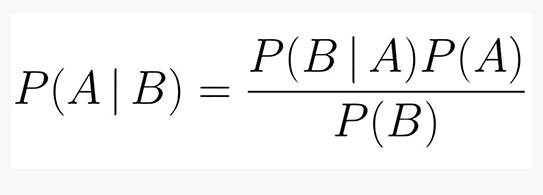
Diagnosi malattia rara.

Supponiamo di avere una malattia rara che colpisce l'1% della popolazione.
Abbiamo anche un test diagnostico per questa malattia che ha una sensibilità del 90% (la probabilità che il test sia positivo dato che il paziente ha effettivamente la malattia)
Una specificità del 95% (la probabilità che il test sia negativo dato che il paziente non ha la malattia).

Vogliamo calcolare la probabilità che un paziente abbia effettivamente la malattia dato che il test è risultato positivo.

Denotiamo con A l'evento "il paziente ha la malattia" e con B l'evento "il test è risultato positivo".
La formula del teorema di Bayes è:
P(A|B) = (P(B|A) * P(A)) / P(B)
Dove:
- P(A|B) è la probabilità che il paziente abbia la malattia dato che il test è risultato positivo (la quantità che vogliamo calcolare).
- P(B|A) è la sensibilità del test, ovvero la probabilità che il test sia positivo dato che il paziente ha effettivamente la malattia (0.9).
- P(A) è la probabilità che un paziente casuale abbia la malattia (0.01).
- P(B) è la probabilità che il test sia positivo, che può essere calcolata utilizzando la regola delle probabilità totali:

P(B) = P(B|A) * P(A) + P(B|non A) * P(non A)
Dove:
- P(B|non A) è la probabilità che il test sia positivo dato che il paziente non ha la malattia
(1 - specificità, ovvero 0.05).
- P(non A) è la probabilità che un paziente casuale non abbia la malattia (1 - P(A), ovvero 0.99).

Sostituendo i valori nella formula, otteniamo:
P(A|B) = (0.9 * 0.01) / ((0.9 * 0.01) + (0.05 * 0.99))
Calcolando i valori, otteniamo:
P(A|B) ≈ 0.153
Quindi, la probabilità che un paziente abbia effettivamente la malattia dato che il test è risultato positivo è di circa 0.153 o 15.3%.