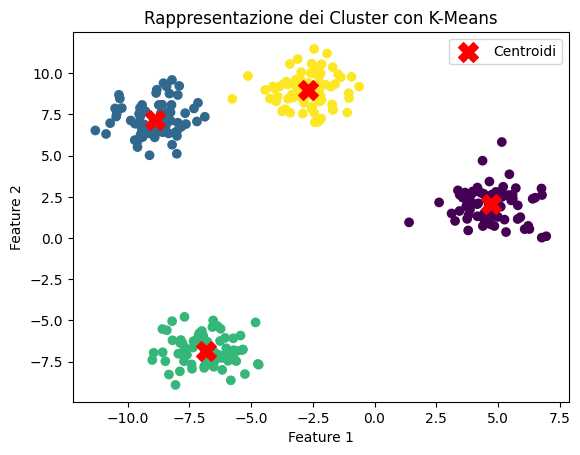
Il metodo k.means
K-means per creare cluster, il coefficiente Silhouette per la metrica
K-Means e Coefficiente di Silhouette
Il K-Means è un algoritmo di clustering non supervisionato che suddivide un insieme di dati in k cluster distinti.L'obiettivo è minimizzare la varianza intra-cluster (distanza tra i punti e il centroide del cluster) e massimizzare la distanza inter-cluster (separazione tra i diversi cluster).
I cluster sono formati in base alla similarità, tipicamente misurata utilizzando la distanza Euclidea.
K-Means cerca di suddividere i dati in gruppi omogenei, detti cluster, in base alla loro somiglianza.
Questo significa che:
- All'interno dello stesso cluster: I punti sono più simili tra loro, secondo una metrica scelta (es. distanza Euclidea), perché sono vicini al centroide del cluster, che rappresenta il punto medio.
- Tra cluster diversi: I punti sono più dissimili, poiché appartengono a gruppi separati, ciascuno con un proprio centroide lontano dagli altri.
Il metodo K-Means utilizza un processo iterativo per identificare i cluster nei dati.
Ecco i passaggi dettagliati delle iterazioni:
-
Inizializzazione:
Scegli casualmente k centroidi iniziali (punti che rappresentano il centro dei cluster).
-
Assegnazione dei punti ai cluster:
- Calcola la distanza tra ogni punto e ciascun centroide utilizzando una metrica (es. distanza Euclidea).
- Assegna ogni punto al cluster del centroide più vicino.
-
Aggiornamento dei centroidi:
- Per ciascun cluster, calcola il nuovo centroide come la media dei punti assegnati a quel cluster (coordinate medie dei punti).
-
Ripetizione:
- Ripete i passaggi 2 e 3 fino a raggiungere la convergenza:
- I centroidi non cambiano più (o cambiano di una quantità trascurabile).
- Non ci sono più variazioni nell'assegnazione dei punti ai cluster.
- Un criterio di stop (es. numero massimo di iterazioni) è raggiunto.
Nota Il processo garantisce la convergenza a un minimo locale dell'obiettivo di ottimizzazione, che consiste nel minimizzare la varianza intra-cluster (somma delle distanze al quadrato dei punti dai rispettivi centroidi).
Coefficiente di Silhouette
E' una misura che valuta la qualità di un clustering.Per ogni punto, confronta la coesione (quanto è vicino agli altri punti del suo cluster) con la separazione (quanto è distante dai punti del cluster più vicino).
Varia tra -1 e 1.
- 1: Il punto è ben assegnato al suo cluster.
- 0: Il punto è al confine tra cluster.
- -1: Il punto è assegnato al cluster sbagliato.
Esempio con K-Means e Coefficiente di Silhouette
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score, silhouette_samples
import numpy as np
# Genera dati sintetici
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)
# Trova il miglior numero di cluster con il metodo del gomito
inertia = []
for n_clusters in range(2, 11):
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
kmeans.fit(X)
inertia.append(kmeans.inertia_)
# Visualizza il grafico del metodo del gomito
plt.plot(range(2, 11), inertia, marker='o')
plt.xlabel('Numero di Cluster')
plt.ylabel('Varianza Inertia')
plt.title('Metodo del Gomito per il K-Means')
plt.show()
# Seleziona il numero ottimale di cluster (nel nostro caso, 4)
optimal_clusters = 4
# Applica K-Means con il numero ottimale di cluster
kmeans = KMeans(n_clusters=optimal_clusters, random_state=42)
labels = kmeans.fit_predict(X)
# Calcola il coefficiente di Silhouette
silhouette_avg = silhouette_score(X, labels)
print(f'Il coefficiente di Silhouette medio è {silhouette_avg:.2f}')
# Calcola il coefficiente di Silhouette per ciascun campione
sample_silhouette_values = silhouette_samples(X, labels)
# Visualizza i risultati
fig, ax = plt.subplots()
y_lower = 10
for i in range(optimal_clusters):
ith_cluster_silhouette_values = sample_silhouette_values[labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = plt.cm.nipy_spectral(float(i) / optimal_clusters)
ax.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
ax.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
ax.set_title("Rappresentazione del coefficiente di Silhouette per ciascun cluster")
ax.set_xlabel("Valore del coefficiente di Silhouette")
ax.set_ylabel("Etichetta del Cluster")
# Linea che indica il coefficiente di Silhouette medio su tutti i dati
ax.axvline(x=silhouette_avg, color="red", linestyle="--")
plt.show()
Coefficiente di Silhouette
Il coefficiente silhouette è una misura di validità interna per valutare la coesione e la separazione dei cluster ottenuti da un algoritmo di clustering, come K-Means. Questa metrica fornisce un'indicazione sulla qualità della suddivisione dei dati nei cluster.Il coefficiente silhouette varia da -1 a 1, dove:
- Valori vicini a 1 indicano che l'istanza è ben collocata nel suo cluster e separata dagli altri.
- Valori vicini a 0 indicano che l'istanza è sulla soglia tra due cluster.
- Valori vicini a 0 indicano che l'istanza è sulla soglia tra due cluster.