Determinazione del Numero Ottimale di Cluster

Determinazione del Numero Ottimale di Cluster con il Metodo della Silhouette
Il metodo della silhouette è un approccio utile per determinare il numero ottimale di cluster in un dataset.
La silhouette misura quanto un punto è simile al proprio cluster rispetto agli altri cluster. Il valore della silhouette varia da -1 a 1
- Un valore vicino a 1 indica che il punto è ben assegnato al suo cluster.
- Un valore vicino a 0 indica che il punto è al confine tra due cluster.
- Un valore negativo indica che il punto potrebbe essere assegnato al cluster sbagliato.

Implementazione del Metodo della Silhouette

Useremo il dataset del vino, applicheremo la standardizzazione e la PCA come nei passi precedenti.
Poi, calcoleremo i valori della silhouette per diversi numeri di cluster e visualizzeremo il grafico della silhouette.

import pandas as pd
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import numpy as np

# Caricamento del dataset del vino
wine = load_wine()
X = wine.data
y = wine.target

# Standardizzazione dei dati
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Applicazione della PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# Funzione per calcolare e visualizzare il grafico della silhouette per vari cluster
def silhouette_analysis(X, range_n_clusters):
    silhouette_avg_values = []
    for n_clusters in range_n_clusters:
        # Applicazione del K-Means clustering
        kmeans = KMeans(n_clusters=n_clusters, random_state=42)
        cluster_labels = kmeans.fit_predict(X)

        # Calcolo del coefficiente della silhouette
        silhouette_avg = silhouette_score(X, cluster_labels)
        silhouette_avg_values.append(silhouette_avg)
        print(f"Per {n_clusters} cluster, il punteggio medio della silhouette è {silhouette_avg}")

        # Creazione del plot della silhouette
        fig, ax1 = plt.subplots(1, 1)
        fig.set_size_inches(10, 7)

        ax1.set_xlim([-0.1, 1])
        ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])

        # Calcolo dei valori della silhouette per ogni punto
        sample_silhouette_values = silhouette_samples(X, cluster_labels)

        y_lower = 10
        for i in range(n_clusters):
            ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
            ith_cluster_silhouette_values.sort()

            size_cluster_i = ith_cluster_silhouette_values.shape[0]
            y_upper = y_lower + size_cluster_i

            color = plt.cm.nipy_spectral(float(i) / n_clusters)
            ax1.fill_betweenx(np.arange(y_lower, y_upper),
                              0, ith_cluster_silhouette_values,
                              facecolor=color, edgecolor=color, alpha=0.7)

            ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

            y_lower = y_upper + 10

        ax1.set_title(f"Grafico della silhouette per {n_clusters} cluster")
        ax1.set_xlabel("Valore del coefficiente della silhouette")
        ax1.set_ylabel("Cluster")

        ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
        ax1.set_yticks([])
        ax1.set_xticks(np.arange(-0.1, 1.1, 0.2))

        plt.show()

    return silhouette_avg_values

# Applicazione della silhouette analysis per un range di cluster
range_n_clusters = [2, 3, 4, 5, 6]
silhouette_avg_values = silhouette_analysis(X_pca, range_n_clusters)

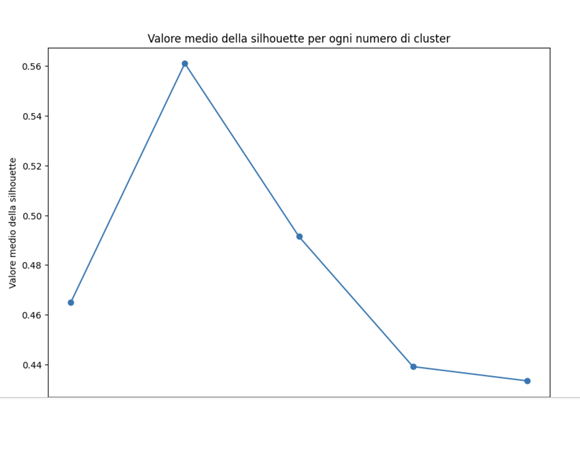
# Visualizzazione del valore medio della silhouette per ogni numero di cluster
plt.figure(figsize=(10, 7))
plt.plot(range_n_clusters, silhouette_avg_values, marker='o')
plt.title('Valore medio della silhouette per ogni numero di cluster')
plt.xlabel('Numero di cluster')
plt.ylabel('Valore medio della silhouette')
plt.show()

Spiegazione Teorica del Metodo della Silhouette

Il metodo della silhouette fornisce una misura di coesione e separazione dei cluster:
- Coefficiente della silhouette Per ogni punto, il coefficiente della silhouette è definito come:
\[ s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))} \]
dove:
\(a(i)\) è la distanza media tra il punto (i) e tutti gli altri punti del suo cluster.
\(b(i)\) è la distanza media tra il punto (i) e tutti i punti del cluster più vicino di cui (i) non fa parte.
Un valore della silhouette vicino a 1 indica che il punto è ben assegnato al cluster giusto, mentre un valore vicino a -1 indica una probabile assegnazione errata.

Silhouette media La silhouette media su tutti i punti del dataset fornisce una misura complessiva della qualità del clustering. Più alto è il valore medio, migliore è la coesione interna dei cluster e la separazione tra di essi.