Bias

Il bias rappresenta l'errore introdotto dal modello a causa delle sue semplificazioni eccessive.
Un modello con alto bias tende a sottostimare o sovrastimare sistematicamente il valore target.
Ad esempio, un modello di regressione lineare applicato a dati con una relazione non lineare avrà un bias elevato perché non sarà in grado di catturare la complessità dei dati.

Varianza

La varianza rappresenta la sensibilità del modello alle variazioni nei dati di addestramento.
Un modello con alta varianza tende a adattarsi eccessivamente ai dati di addestramento.
Il modello ha una scarsa capacità di generalizzazione su nuovi dati.
Un modello ad alta varianza può adattarsi eccessivamente ai dati di addestramento, catturando rumore e pattern casuali, ma può non generalizzare bene su nuovi dati.

Overfitting

L'overfitting si verifica quando il modello ha una varianza elevata e un bias basso.
Questo accade quando il modello è troppo complesso rispetto alla complessità intrinseca dei dati di addestramento.
In pratica, il modello si adatta troppo ai dati di addestramento, catturando anche il rumore e portando a prestazioni scadenti su dati non visti.

Underfitting

L'underfitting si verifica quando il modello ha un bias elevato e una varianza bassa.
Questo accade quando il modello è troppo semplice rispetto alla complessità intrinseca dei dati di addestramento.
In pratica, il modello non è in grado di catturare correttamente la struttura dei dati di addestramento, portando a prestazioni scadenti sia sui dati di addestramento che su quelli di test.

In sintesi, il bias e la varianza sono due componenti che contribuiscono alla complessità complessiva del modello.
L'overfitting si verifica quando c'è un eccesso di varianza rispetto al bias, mentre l'underfitting si verifica quando c'è un eccesso di bias rispetto alla varianza.

Trovare un equilibrio tra bias e varianza è cruciale per ottenere un modello che generalizzi bene su dati non visti.

Una rete neurale che soffra di overfitting, ha una elevata complessità del modello aggiungendo un numero eccessivo di strati o di nodi.
Il numero di dati di addestramento disponibili è ridotto con un rumore nei dati di addestramento.
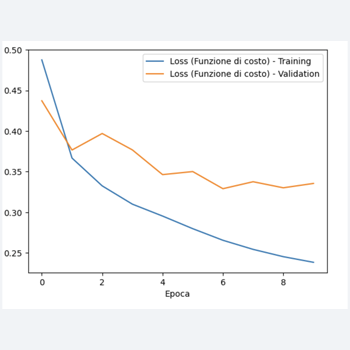
Ecco un esempio di una rete neurale che soffra di overfitting utilizzando il dataset Fashion MNIST.

import numpy as np
from keras.datasets import fashion_mnist
from keras.models import Sequential
from keras.layers import Flatten, Dense
from keras.optimizers import Adam

# Caricamento del dataset
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()

# Normalizzazione dei valori dei pixel
X_train = X_train / 255.0
X_test = X_test / 255.0

# Creazione della rete neurale
model = Sequential([
    Flatten(input_shape=(28, 28)),
    Dense(512, activation='relu'),
    Dense(512, activation='relu'),
    Dense(512, activation='relu'),
    Dense(10, activation='softmax')
])

# Compilazione del modello con Adam come ottimizzatore
model.compile(optimizer=Adam(), loss='sparse_categorical_crossentropy', metrics=['accuracy'])

# Addestramento del modello
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_test, y_test))

# Valutazione del modello
train_loss, train_acc = model.evaluate(X_train, y_train, verbose=0)
test_loss, test_acc = model.evaluate(X_test, y_test, verbose=0)

print(f'Loss e accuratezza sul training set: {train_loss}, {train_acc}')
print(f'Loss e accuratezza sul test set: {test_loss}, {test_acc}')

In questo esempio, abbiamo creato una rete neurale con tre strati densi da 512 nodi ciascuno.
Questa architettura complessa può portare all'overfitting, specialmente se il dataset di addestramento non è sufficientemente grande.

Al termine della esecuzione del costo, avremo:
Loss e accuratezza sul training set: 0.22695335745811462, 0.9144666790962219
Loss e accuratezza sul test set: 0.3916592597961426, 0.8840000033378601

Cioe' una funzione di costo maggiore nel data set di TEST
Questa misurazione consente di verificare se un modello è in overfitting