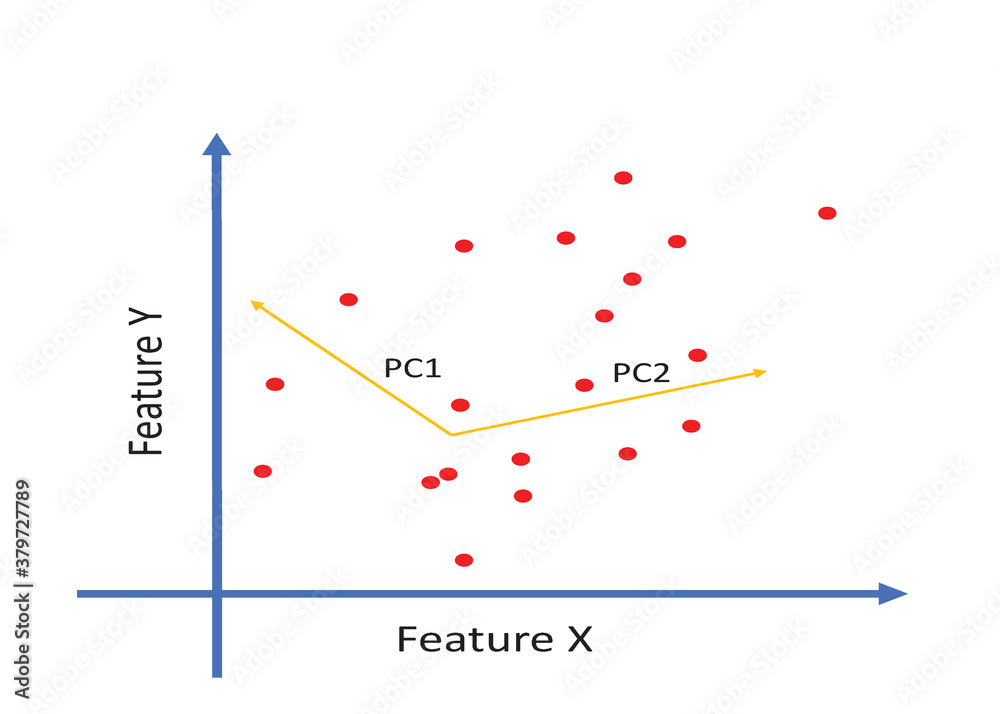
Principal Component Analysis (PCA)

La Principal Component Analysis (PCA) è una tecnica di riduzione delle dimensioni utilizzata nell'analisi dei dati per identificare pattern e relazioni nei dati stessi.
L'obiettivo è quello di ridurre il numero di variabili mantenendo al contempo la maggior parte delle informazioni.

La Principal Component Analysis (PCA) è una tecnica di riduzione delle dimensioni utilizzata per comprimere un grande numero di variabili in un numero minore di variabili, chiamate componenti principali, mantenendo al contempo la maggior parte della varianza nei dati originali.
Il principio di base della PCA è quello di trovare una trasformazione lineare delle variabili originali in un nuovo set di variabili (le componenti principali) che massimizzano la varianza

Esempio PCA

Ecco un esempio di come eseguire la PCA in Python utilizzando il modulo `PCA` di scikit-learn:

import numpy as np
from sklearn.decomposition import PCA

# Creazione di un dataset di esempio
data = np.random.rand(100, 5)  # 100 campioni, 5 variabili

# Inizializzazione dell'oggetto PCA
pca = PCA(n_components=2)  # Riduzione a 2 componenti principali

# Addestramento del modello PCA
pca.fit(data)

# Trasformazione del dataset originale
data_pca = pca.transform(data)

# Stampa delle prime 5 righe del dataset originale
print("Dataset originale:")
print(data[:5, :])

# Stampa delle prime 5 righe del dataset dopo la PCA
print("\nDataset dopo PCA:")
print(data_pca[:5, :])

In questo esempio, `n_components` specifica il numero di componenti principali desiderate. Dopo aver addestrato il modello PCA con i dati originali, la funzione `transform` viene utilizzata per ridurre le dimensioni del dataset originale secondo le componenti principali identificate.

I risultati possono essere interpretati osservando la riduzione delle dimensioni del dataset.
Ad esempio, se `n_components` è impostato su 2, il dataset ridotto conterrà solo due variabili anziché le cinque originali.
La PCA cerca di mantenere la maggior parte della varianza nei dati, quindi le prime componenti principali racconteranno la maggior parte della variabilità nei dati originali.