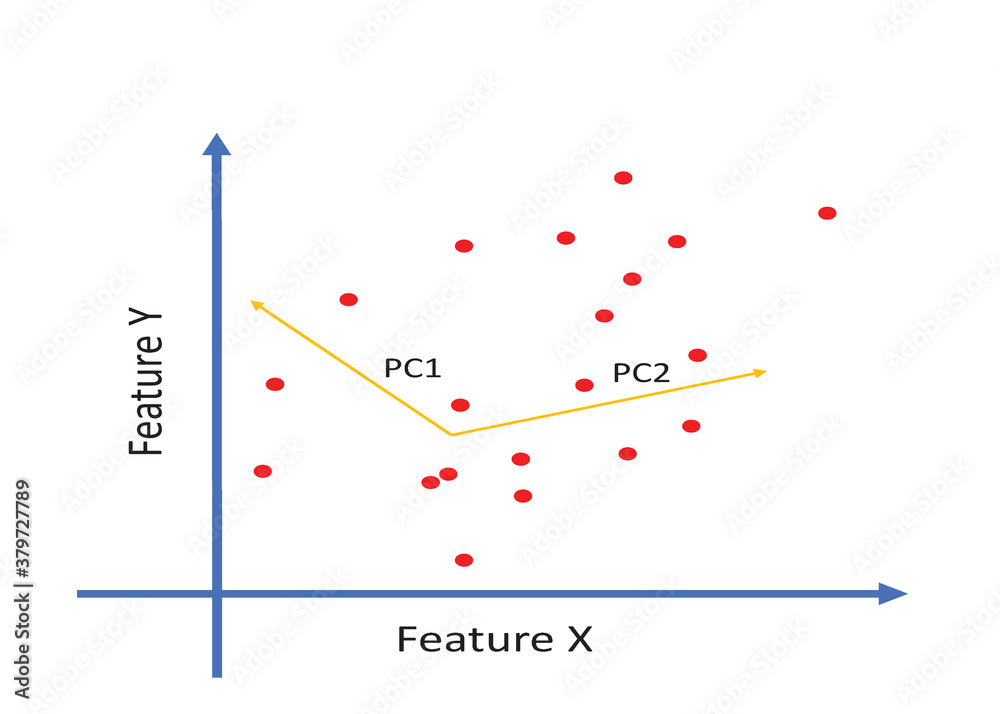
Kernel PCA
Un'estensione della PCA che utilizza tecniche di kernel per eseguire una trasformazione non lineare dei dati.
Cos'è la Kernel PCA?
La Kernel Principal Component Analysis (Kernel PCA) è un'estensione della Principal Component Analysis (PCA) che utilizza tecniche di kernel per eseguire una trasformazione non lineare dei dati. La PCA tradizionale è una tecnica di riduzione della dimensionalità che trova le componenti principali linearmente più significative dei dati. Tuttavia, la PCA standard può risultare inefficace quando i dati non sono linearmente separabili. La Kernel PCA affronta questo problema trasformando i dati originali in uno spazio a dimensioni superiori utilizzando una funzione kernel. In questo spazio ad alta dimensione, è più probabile che i dati siano linearmente separabili. Dopo la trasformazione, la PCA viene applicata in questo spazio trasformato per trovare le componenti principali.
Quando si usa la Kernel PCA
La Kernel PCA è utile quando:
- I dati hanno una struttura non lineare.
- La PCA tradizionale non riesce a separare efficacemente i dati.
- Si desidera ridurre la dimensionalità dei dati mantenendo informazioni non lineari.
- È necessario visualizzare dati complessi in uno spazio bidimensionale o tridimensionale.
Esempio con Python
Vediamo un esempio pratico utilizzando Python.Utilizzeremo la funzione `make_circles` di `sklearn.datasets` per generare un dataset di dati non linearmente separabili, lo visualizzeremo usando Seaborn e applicheremo la Kernel PCA per renderli separabili.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_circles
from sklearn.decomposition import KernelPCA
from sklearn.preprocessing import StandardScaler
# Generazione del dataset
X, y = make_circles(n_samples=200, factor=.05, noise=.1, random_state=1)
# Visualizzazione del dataset originale
plt.figure(figsize=(8, 6))
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette='viridis')
plt.title('Dataset originale non linearmente separabile')
plt.show()
# Standardizzazione dei dati
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Applicazione della Kernel PCA
kpca = KernelPCA(kernel='rbf', fit_inverse_transform=True, gamma=15, n_components=2)
X_kpca = kpca.fit_transform(X_scaled)
# Visualizzazione dei dati trasformati
plt.figure(figsize=(8, 6))
sns.scatterplot(x=X_kpca[:, 0], y=X_kpca[:, 1], hue=y, palette='viridis')
plt.title('Dataset trasformato con Kernel PCA')
plt.show()
Spiegazione del Codice
- Generazione del Dataset**: Utilizziamo `make_circles` per creare un dataset di punti in due cerchi concentrici, che non sono linearmente separabili.
- Visualizzazione del Dataset Originale**: Utilizziamo Seaborn per visualizzare il dataset originale. Come previsto, i punti dei due cerchi si sovrappongono, rendendo difficile la separazione lineare.
- Standardizzazione dei Dati**: La standardizzazione è un passaggio importante per le tecniche di kernel, in quanto migliora la performance della trasformazione kernel.
- Applicazione della Kernel PCA**: Applichiamo la Kernel PCA con un kernel RBF (Radial Basis Function) per trasformare i dati in uno spazio ad alta dimensione in cui i due cerchi sono linearmente separabili.
- Visualizzazione dei Dati Trasformati**: Visualizziamo i dati trasformati. Dopo l'applicazione della Kernel PCA, i due gruppi di punti sono chiaramente separabili, dimostrando l'efficacia della tecnica su dati non linearmente separabili.