La regolarizzazione dei dati è una tecnica utilizzata per ridurre l'overfitting in modelli di machine learning.
L'overfitting si verifica quando il modello si adatta eccessivamente ai dati di addestramento, perdendo di generalità e capacità di generalizzazione su nuovi dati.
La regolarizzazione introduce penalità sui coefficienti del modello, limitandone l'importanza eccessiva attribuita a specifici attributi o caratteristiche dei dati.

Le due tecniche di regolarizzazione più comuni sono la regolarizzazione L1 e L2.
-La regolarizzazione L1 (lasso) aggiunge la somma assoluta dei valori assoluti dei coefficienti.
-La regolarizzazione L2 (ridge) aggiunge la somma dei quadrati dei coefficienti.

La regolarizzazione L1 tende a produrre modelli sparsi, cioè con molti coefficienti nulli, mentre la regolarizzazione L2 tende a mantenere tutti i coefficienti, anche se li riduce in modo proporzionale.

La regolarizzazione Elastic Net combina la regolarizzazione L1 e L2, fornendo un controllo flessibile sulla selezione delle caratteristiche e sulla riduzione del coefficiente.
L'elastic net utilizza un parametro di mescolanza per bilanciare l'effetto di L1 e L2.

Di seguito un esempio di come applicare la regolarizzazione Elastic Net in Python utilizzando Scikit-Learn:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import r2_score

# Genera il dataset casuale
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 1) * 10
y = X ** 2 + 3 * X + np.random.randn(n_samples, 1) * 5  # Relazione non lineare

# Dividi il dataset in training e test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Normalizza i dati
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# Regressione polinomiale con regolarizzazione ElasticNet
poly = PolynomialFeatures(degree=2)
X_train_poly = poly.fit_transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)



model = ElasticNet(alpha=0.7, l1_ratio=0.5, max_iter=10000)
model.fit(X_train_poly, y_train)

# Calcola l'indicatore R^2
y_train_pred = model.predict(X_train_poly)
y_test_pred = model.predict(X_test_poly)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)

# Stampare i valori R^2
print(f'R^2 sul training set: {r2_train:.3f}')
print(f'R^2 sul test set: {r2_test:.3f}')

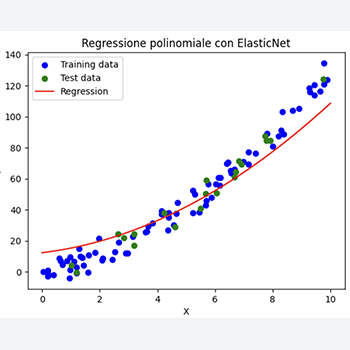
# Grafico del dataset e della regressione
plt.scatter(X_train, y_train, color='blue', label='Training data')
plt.scatter(X_test, y_test, color='green', label='Test data')
x_values = np.linspace(0, 10, 100)
X_values_scaled = scaler.transform(x_values.reshape(-1, 1))
X_values_poly = poly.transform(X_values_scaled)
y_values_pred = model.predict(X_values_poly)
plt.plot(x_values, y_values_pred, color='red', label='Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Regressione polinomiale con ElasticNet')
plt.legend()
plt.show()

Questo codice genera un dataset con una relazione non lineare tra X e y, applica la normalizzazione dei dati e la regressione polinomiale con regolarizzazione ElasticNet.
Infine, stampa i valori R^2 per valutare le prestazioni del modello.