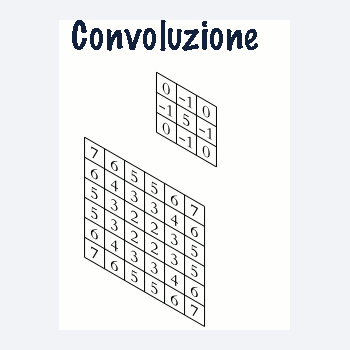
Convoluzione
Il Principio di base delle CNN è la Convoluzione
Le reti neurali convoluzionali (CNN) sono un tipo di rete neurale profonda progettata principalmente per analizzare dati a griglia, come immagini e video.
Sono state ispirate dalla struttura e dal funzionamento del sistema visivo biologico degli animali.
Principio di base delle CNN è la Convoluzione
La convoluzione è l'operazione fondamentale delle reti neurali convoluzionali (CNN).In termini matematici, la convoluzione discreta tra una matrice di input (spesso rappresentante un'immagine) e un filtro (o kernel).
Supponiamo di avere una matrice di input \( I \) di dimensioni \( m \times n \) e un filtro \( K \) di dimensioni \( p \times q \). L'operazione di convoluzione tra \( I \) e \( K \), indicata come \( I * K \), produce una matrice di output \( O \) di dimensioni \( (m-p+1) \times (n-q+1) \), calcolata come segue:
\[ O(i, j) = \sum_{u=0}^{p-1} \sum_{v=0}^{q-1} I(i+u, j+v) \cdot K(u, v) \]
Dove:
- \( O(i, j) \) è il valore nella posizione \( (i, j) \) della matrice di output \( O \).
- \( I(i+u, j+v) \) rappresenta il valore dell'elemento nella matrice di input \( I \) nella posizione \( (i+u, j+v) \).
- \( K(u, v) \) è il valore del filtro nella posizione \( (u, v) \).
- La sommatoria scorre su tutti gli indici validi \( u \) e \( v \) del filtro.
Questa formula calcola il prodotto punto tra il filtro e una porzione corrispondente dell'input, e quindi somma i risultati per ottenere un singolo valore nell'output. Questo processo viene ripetuto scorrendo il filtro sull'intera matrice di input.
Un aspetto importante della convoluzione è che il filtro viene condiviso su tutta la matrice di input durante il processo di convoluzione. Ciò significa che gli stessi pesi vengono utilizzati per calcolare ogni valore dell'output, il che porta a una riduzione del numero di parametri rispetto a una rete neurale completamente connessa.
In pratica, durante l'applicazione delle CNN alle immagini, il filtro (o kernel) scorrerà sull'intera immagine, calcolando il prodotto punto con i pixel sovrapposti e sommandoli per produrre un valore nell'output.
Questo processo viene ripetuto per ogni posizione dell'immagine, generando così una "mappa delle caratteristiche" che cattura le informazioni rilevanti dell'immagine.
Vantaggi delle CNN rispetto alle reti neurali classiche
-
Invarianza spaziale: Le CNN sono in grado di riconoscere pattern in immagini indipendentemente dalla loro posizione, grazie all'uso delle operazioni di convoluzione e pooling.
-
Riduzione del numero di parametri: Le CNN sfruttano la condivisione dei pesi attraverso i vari strati, riducendo significativamente il numero di parametri rispetto alle reti neurali completamente collegate, il che le rende più efficienti in termini computazionali.
-
Riduzione del rischio di overfitting: L'uso di pooling e l'introduzione di non linearità attraverso strati di attivazione come ReLU aiutano a ridurre il rischio di overfitting.
Quando usarle rispetto alle reti neurali classiche
Le CNN sono particolarmente efficaci quando si lavora con dati a griglia come immagini, video o dati spaziali in generale.Sono preferite rispetto alle reti neurali classiche quando si tratta di problemi di computer vision, riconoscimento di immagini, segmentazione, classificazione di immagini, ecc.
Le reti neurali classiche, d'altra parte, possono essere più adatte per dati non strutturati o sequenziali, come il linguaggio naturale o i dati temporali.