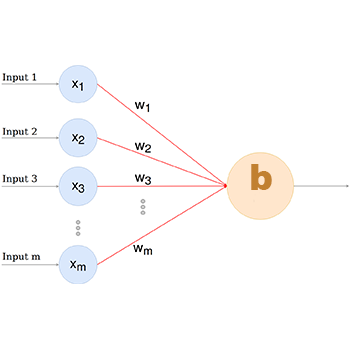
Funzione di Attivazione
Le funzioni di attivazione fondamentali nelle reti neurali perché introducono non linearità nel modello.
Le funzioni di attivazione sono fondamentali nelle reti neurali perché introducono non linearità nel modello, consentendo alla rete di apprendere relazioni complesse nei dati.
Ogni funzione di attivazione ha un diverso comportamento e può essere utilizzata in base alle specifiche del problema e alle caratteristiche dei dati.
Di seguito, descriverò utilizzo, formula e criteri di scelta per alcune delle funzioni di attivazione più comuni:
Sigmoid (Sigmoide)
- Utilizzo: Utilizzato principalmente negli strati di output delle reti neurali binarie, dove l'obiettivo è la classificazione binaria.- Formula: \( \sigma(x) = \frac{1}{1 + e^{-x}} \)
- Criteri di scelta: Da utilizzare quando si ha la necessità di mappare l'output in un intervallo compreso tra 0 e 1, adatto per la classificazione binaria.
Tanh (Tangente iperbolica)
- Utilizzo: È simile alla sigmoide, ma mappa l'output nell'intervallo compreso tra -1 e 1, ed è spesso utilizzato negli strati nascosti delle reti neurali.
- Formula: \( \text{tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \)
- Criteri di scelta: È preferito rispetto alla sigmoide quando si desidera una maggiore sensibilità nei valori negativi e positivi, adatto per problemi di classificazione multiclasse.
ReLU (Rectified Linear Unit
- Utilizzo: È diventato uno dei più popolari nelle reti neurali grazie alla sua semplicità e alle ottime prestazioni in molti casi.
- Formula: \( \text{ReLU}(x) = \max(0, x) \)
- Criteri di scelta: È preferito in molti casi grazie alla sua semplicità e all'eliminazione del problema del gradiente sparito.
È particolarmente efficace nelle reti profonde.
Leaky ReLU
- Utilizzo: Simile a ReLU, ma risolve il problema di "dying ReLU" introducendo una piccola pendenza negativa per i valori negativi di input.- Formula: \( \text{LeakyReLU}(x) = \begin{cases} x & \text{se } x > 0 \\ \text{alpha} \cdot x & \text{altrimenti} \end{cases} \), dove alpha è un valore piccolo positivo.
- Criteri di scelta: Da utilizzare quando si vuole risolvere il problema di "dying ReLU", soprattutto se si hanno molti neuroni che diventano inattivi durante l'addestramento.
La funzione di attivazione identità, che è essenzialmente una funzione lineare \(f(x) = x\), non introduce non linearità.
Viene utilizzata principalmente negli strati di output per problemi di regressione, dove si desidera una previsione diretta del valore di output senza alcuna trasformazione.