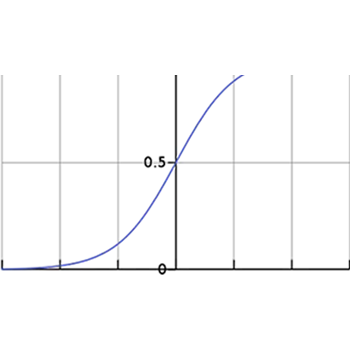
Softmax
La funzione di attivazione softmax utilizzata per classificazione multiclasse
Funzione Soft Max
La funzione di attivazione softmax è comunemente utilizzata negli strati di output delle reti neurali per problemi di classificazione multiclasse. La sua principale caratteristica è quella di convertire un vettore di valori in input in un vettore di probabilità normalizzate, dove la somma di tutte le probabilità è uguale a 1. Questa caratteristica rende la funzione softmax ideale per la classificazione multiclasse, poiché fornisce una distribuzione di probabilità su più classi.
Formula della funzione softmax per un vettore di input \( \mathbf{z} = (z_1, z_2, ..., z_n) \):
\[ \text{softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}} \]
Dove:
- \( \text{softmax}(\mathbf{z})_i \) rappresenta l'i-esimo elemento del vettore di output softmax.
- \( e \) è la costante di Nepero (e = 2.71828...).
- \( z_i \) è l'i-esimo elemento del vettore di input \( \mathbf{z} \).
- \( \sum_{j=1}^{n} e^{z_j} \) rappresenta la somma degli esponenziali di tutti gli elementi del vettore di input.
La funzione softmax produce valori compresi tra 0 e 1 e assicura che la somma di tutti i valori nel vettore di output sia sempre uguale a 1.
Questo la rende particolarmente utile per la classificazione multiclasse, dove ogni classe è associata a una probabilità di appartenenza.
La classe con la probabilità più alta viene quindi scelta come output della rete neurale per un dato input.