Support Vector Machine nei problemi di regressione

La Support Vector Machine (SVM) nei problemi di regressione è chiamata Support Vector Regression (SVR).
L'obiettivo dell'SVR è trovare una funzione che si avvicini il più possibile ai target dei dati di addestramento, mantenendo allo stesso tempo un margine di tolleranza (epsilon) entro il quale le predizioni possono discostarsi dal target senza penalità.
L'SVR cerca di bilanciare la complessità del modello e l'accuratezza del fit, trovando una soluzione che minimizzi l'errore di predizione con una penalità per la complessità.

Quando si usa l'SVR

L'SVR è utile quando:
- Si desidera fare previsioni di valori continui.
- Si ha un dataset con rumore e si desidera trovare una funzione di regressione che sia robusta.
- Si vuole controllare il compromesso tra il fit del modello e la sua complessità.

Esempi in Python usando SVR con kernel lineare, polinomiale e RBF

Caricamento e Split del Dataset

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Generazione del dataset
np.random.seed(42)
X = np.sort(np.random.rand(40, 1) * 4, axis=0)
y = 10 * np.sin(X).ravel()

# Visualizzazione del dataset
plt.figure(figsize=(7, 6))
plt.scatter(X, y, color='red', label='Dati originali')
plt.title('Dataset originale')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

Modello SVR con Kernel Lineare

# Divisione del dataset in training e test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Modello SVR con kernel lineare
svr_linear = SVR(kernel='linear')
svr_linear.fit(X_train, y_train)
y_pred_linear = svr_linear.predict(X_test)

# Calcolo dell'errore quadratico medio (MSE)
mse_linear = mean_squared_error(y_test, y_pred_linear)
print("SVR Lineare MSE:", mse_linear)

# Visualizzazione della retta di separazione
plt.figure(figsize=(7, 6))
plt.scatter(X_test, y_test, color='red', label='Dati reali')
plt.plot(X_test, y_pred_linear, color='blue', label='Predizioni SVR Lineare')
plt.title('SVR con Kernel Lineare')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

Modello SVR con Kernel Polinomiale

# Modello SVR con kernel polinomiale
svr_poly = SVR(kernel='poly', degree=2, C=1e3)
svr_poly.fit(X, y)
y_pred_poly = svr_poly.predict(X)

# Calcolo dell'errore quadratico medio (MSE)
mse_poly = mean_squared_error(y, y_pred_poly)
print("SVR Polinomiale MSE:", mse_poly)

# Visualizzazione della retta di separazione
plt.figure(figsize=(7, 6))
plt.scatter(X, y, color='red', label='Dati reali')
plt.plot(X, y_pred_poly, color='blue', label='Predizioni SVR Polinomiale')
plt.title('SVR con Kernel Polinomiale')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

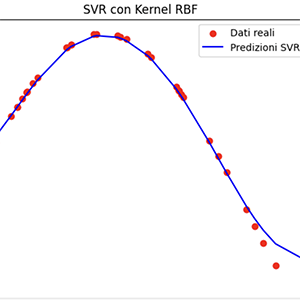
Modello SVR con Kernel RBF

# Modello SVR con kernel RBF
svr_rbf = SVR(kernel='rbf')
svr_rbf.fit(X, y)
y_pred_rbf = svr_rbf.predict(X)

# Calcolo dell'errore quadratico medio (MSE)
mse_rbf = mean_squared_error(y, y_pred_rbf)
print("SVR RBF MSE:", mse_rbf)

# Visualizzazione della retta di separazione
plt.figure(figsize=(7, 6))
plt.scatter(X, y, color='red', label='Dati reali')
plt.plot(X, y_pred_rbf, color='blue', label='Predizioni SVR RBF')
plt.title('SVR con Kernel RBF')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()